去年搞了一个极空间Z2Pro，于是就想着把之前的svn库从移动硬盘转移到jZ2pro上。

More...

photon是德国Exit Games开发的一套网络同步框架，也叫photon engine。

这家公司有着15年以上的服务器端开发经验。

属于商业软件，收费。有提供免费的版本

photon产品目前比较有用的是

• Fusion：适用于photon云服务器的Unity状态同步框架

• Quantum：适用于photon云服务器的Unity的ECS同步框架，给予预测回滚机制，适用于对网络延迟较为敏感对游戏，比如体育 moba 赛车 格斗游戏等

More...

在《正整数对的唯一解》一文中，提出了一个问题，对于不同的整数对（a，b）找到唯一的正整数c，这样就可以通过c，一次性的比较不同整数对的大小

其实这个问题的解决方案已经在文中很接近了，就是将2维数据编码为1维表的过程

在询问了ChatGPT之后，我得到了一个关键的词，叫做配对函数

在数学中，配对函数是一种将两个自然数唯一地编码成一个自然数的过程。

More...

简称NeatDM，是一款多线程下载工具和视频嗅探工具

官网：https://www.neatdownloadmanager.com/index.php/en/

特点

• 支持win+mac

More...

失眠，原因很多

昨夜失眠，竟然是因为想到一个数学题

一开始是这样的，双方投掷2个骰子，一般的规则就是每个人用加法把自己的2个骰子点数加起来，然后比大小

但是有时候会出现双方相同的情况，比如1+6和2+5

所以就在想，如果排除掉点数完全一样的情况下，有没有一种数学算法，可以一次计算比出大小

扩展和归纳起来就是：

对于一个整数对a,b（ab不分先后，即1/6和6/1视为同一个整数对），设计一种算法，使得对于不同的整数对，计算出来的结果为整数且唯一？

想不到好的办法，一开始先试试乘法即f(a,b)=a*b

显然，这个算法很快就被排除了，原因很简单，比如2*3=1*6或者2*2 = 1*4

既然乘法不行，是不是可以和加法结合起来呢，比如f(a,b)=a*b+a+b

睡不着，想了2个小时，发现一个反例，2*3+2+3 = 11 = 1*5+1+5

好吧，自己解决不了，就去请求万能的朋友圈

恍恍惚惚，半睡半醒之间，感觉找到了突破口，就是查二维表

做游戏我们常常会有查表的操作，细细一想，不就是查个二维表么，只要构建一个可以利用一个一元公式构建的二维表就行

比如最简单有序的6*6的表

那么对于每一行a和每一行b就可以得到唯一的解(a-1)*6+b=a*6+b-6，-6不影响所以也可以去掉

这么一推广就可以得到这样的公式

f(a,b)=a*N+b

但是很显然有个问题，比如对于f(a,b)=a*6+b来说

随便取个ab，比如3和4，结果为3*6+4 = 22，那么我也可以a取个2，然后找到b使得结果也为22，即2*6+10=22

难道这样是思路是错误的么？

再看2*6+10这个例子，可以看到原因在于表里面根本就没有第10列，所以数据是超出了查表的范围的

那怎么办？既然超出列数，我们增加列数就可以。让列处于我们可查询的范围内。那么

N的最小值可以等于b。

那么公式就简化为f(a,b)=a*b+b= (a+1)*b

从公式上看就很神奇，之前f(a,b)=a*b不行，但是a加了一个1就可以

那么怎么从数学上证明这个公式是可行的呢？

来个反证法，

如果存在2对不同的整数对(a1,b1)和(a2,b2)，使得(a1+1)*b1 = (a2+1)*b2，那么我们的公式就是错误的，否则肯定是正确的。

好吧，下面不会了，等想到数学证明方法再继续

More...

前言

在unity开发游戏编辑器扩展中，我们常常会用到节点编辑器。节点编辑器就是用节点和节点连接的图形话编辑器，比如unity自带的shadergraph就是一个节点编辑器。用户通过节点之间的拖拖拉拉，连线就能得到想要的结果。

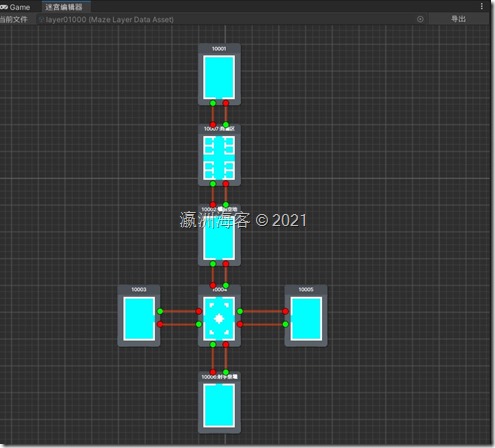
在一段时间里，打算做一个迷宫的地图编辑器，每个地图有上下左右4个门，可以和其他地图连接。于是打算开发一个编辑器，通过可视化的方式去生成整个迷宫的数据。查了很多的节点插件，xnode作为轻量级的节点编辑器就非常适合用来做二次开发

Xnode（https://github.com/Siccity/xNode）是开源的轻量级的节点编辑器插件。所以理解和开发起来非常方便

最终开发效果如下。可以在窗口内创建节点，设置四个门的跳转关系，最终点击导出保存为一个指定的数据文件

More...

2018年，google推出了aab技术。在此之后google发布通知：从 2021 年 8 月起，新应用需要使用 Android App Bundle 才能在 Google Play 中发布。

这意味着以GP为主要平台的海外版本，都需要使用aab。那么什么是aab，和apk有什么不同呢？

aab官方介绍：https://developer.android.com/guide/app-bundle

简单地说aab就是一个带有很多分包数据的压缩包。它将一个apk拆分了多个小包，比如按CPU架构拆分，按语言拆分等等，最终移动设备安装时只需要下载需要的分包即可。

apk可以直接安装到用户的设备上，但是aab只是一种发布格式，所以不能直接安装。但是可以使用bundletool命令行连接设备进行模拟安装

More...

不知道和5月份的血月有没有什么关系，最近好多人的精神和情绪都受到了一定的影响。不过我感觉如果是的话，这个也可能只是一种诱因，更主要的问题还在于自己不好的生活习惯，以及引起的长时间的低质量的睡眠。

突发性的头晕

5月2号早上的时候，刚刚起床在玩手机麻将，突然间就咚的一下，脑袋突然一阵空白。因为就1秒不到就恢复了，当时没在意。

但是在5月7号早上的时候，好好地在听歌写代码，突然间，一阵晕眩感袭来。我飞快地拿下耳机，然后和同事说，我貌似要晕了。同事也吓了一跳，急忙的问我什么情况，然后递给我一瓶可乐，以为是低血糖。休息片刻之后，差不多5秒不到的时间，又恢复了。不过这次让我感觉到慌张，想到了之前网上各种程序员猝死的报导，更是害怕极了。

More...

一次结婚宴

黄叔终于结婚了！10.1大老远从杭州跑到金华浦江参加婚宴。虽然遇到高速入口关闭的情况，还好从下个入口进去了。新郎帅气，新娘也是漂亮，恭喜恭喜！本来聚得就少，以后可能更少了。。。。。。

More...

对于资源加密的思考

       很多人认为ab包不需要加密，但是这样的人我认为，他思考问题的方式是片面的且狭隘。

     是否加密应该根据项目本身的资源价值来决定。是否提高资源的破解难度，比如对于一个没什么价值的项目，也没有人会想要去拿你的资源，自然不需要。但是比如像闪耀暖暖这样，资源密集且开发代价较高的项目，资源应该在一定程度上保护起来，使得破解的代价也得到提高。当然，对于破解高手而言，破解只是时间问题。这里主要的目标还是提高破解的代价。

More...